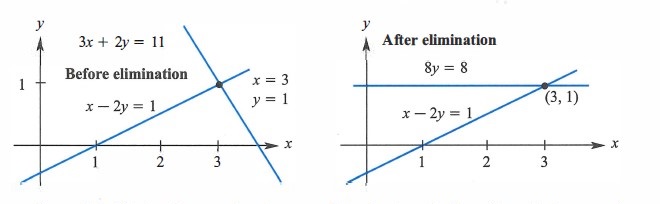
这一节介绍方程组的消元法、矩阵乘法及性质。
第一部分:方程组的消元法
考虑三元一次方程组
$$\begin{array} &x&+&2y&+&z&=&2\\3x&+&8y&+&z&=&12\\& &4y&+&z&=&2\end{array}$$
把它写作 \(AX = b \) 的形式那么它的 \( A \) 就是
$$\begin{bmatrix}1&2&1\\3&8&1\\0&4&1\end{bmatrix}$$
我们把最左上角的 \(1 \) 定为“主元一”,第一行定为主元行。然后,对第二行进行消元,得到下面的矩阵
$$\begin{bmatrix}1&2&1\\0&2&-2\\0&4&1\end{bmatrix}$$
用同样的方法,对第三行消元得到
$$\begin{bmatrix}1&2&1\\0&2&-2\\0&0&5\end{bmatrix}$$
记作矩阵 \(U \)
消元法失效的情况:
- 如果0占据了主元的位置,那么就交换行
- 某行中不存在非0元素时,消元法失效(或者结束)
解方程组:
上面是消元的过程。在解方程组的问题上,需要进行“回代”
在前面的 \(AX = b\) 的矩阵 \(A\) 中,引入右侧向量 \(b\), 构成增广矩阵如下
$$\left[ \begin{array} {ccc|c} 1&2&1&2\\3&8&1&12\\0&4&1&2\end{array} \right]$$
用消元法对这个增广矩阵同步消元,得到
$$\left[ \begin{array} {ccc|c} 1&2&1&2\\0&2&-2&6\\0&0&5&-10\end{array} \right]$$
即为消元后的方程组:
$$\begin{array} &x&+&2y&+&z&=&2\\& &2y&-&2z&=&6\\& & & &5z&=&-10\end{array}$$
解为:\(x=2 , y=1 , z=-2\)
第二部分:用矩阵表示变换
- 矩阵右乘列向量,可以看作是对矩阵的列进行线性组合
- 行向量左乘矩阵,可以看作是对矩阵的行进行线性组合
在进行矩阵乘法时,要注意用向量的角度来思考
对应第一部分里的行变换,应该是:
$$\begin{bmatrix}1&0&0\\-3&1&0\\0&0&1\end{bmatrix} \begin{bmatrix}1&2&1\\3&8&1\\0&4&1\end{bmatrix} = \begin{bmatrix}1&2&1\\0&2&-2\\0&4&1\end{bmatrix}$$
现在矩阵乘法可以有三种方法:
- 用列求
- 用行求
- 用元素乘积的和求(课本里常见)
第三部分:
把初等矩阵记作 —— \(E\)
\(E_{21}\) 表示位置 \((2, 1)\) 上的变换
矩阵消元每一步就是用到一个初等矩阵左乘。
把这些步骤综合起来(仍以第一部分为例):\(E_{32}(E_{21} \cdot A ) = U\)
矩阵乘法的一些性质为:
- 结合律,即若 \(E_{32} ( E_{21} \cdot A ) = U,则 ( E_{32} \cdot E_{21} )A = U\)
很多运算和证明都要用到结合律 - 交换两行的初等矩阵(置换矩阵 P permutation)——“行交换”,即左乘置换矩阵为行交换
$$\begin{bmatrix}0&1\\1&0\end{bmatrix} \begin{bmatrix}a&b\\c&d\end{bmatrix} = \begin{bmatrix}c&d\\a&b\end{bmatrix}$$ - 如果要交换矩阵的列,则右乘置换矩阵
$$\begin{bmatrix}a&b\\c&d\end{bmatrix} \begin{bmatrix}0&1\\1&0\end{bmatrix} = \begin{bmatrix}b&a\\d&c\end{bmatrix}$$ - 矩阵乘法中,结合律是正确的,但交换律却不成立,这说明矩阵乘法的因数顺序是不能改变的。