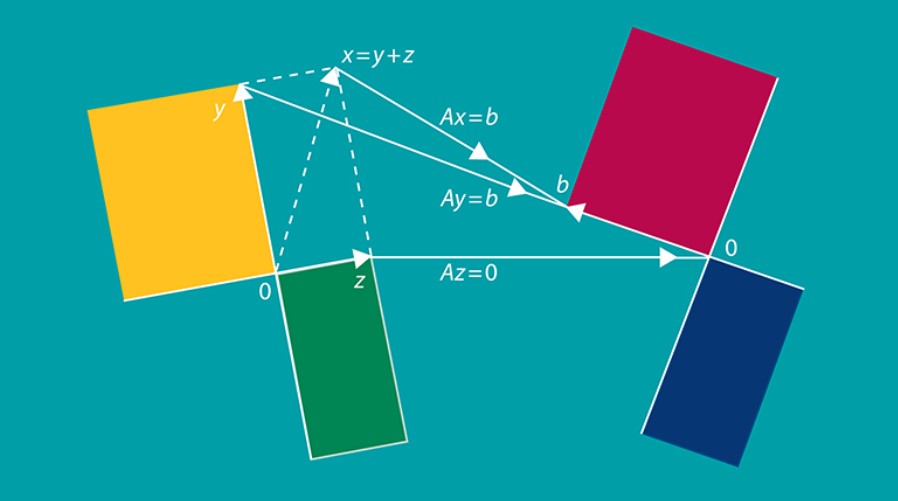
本系列文章记录线性代数的学习笔记。我们从方程组开始吧。
常见的教材如同济版,是从行列式开始。但是这里,我们要换一个路径——从方程组开始。
例1:考虑二元一次方程组
$$\begin{array} &2x&-&y&=&0\\-x&+&2y&=&3\end{array}$$
写成矩阵的形式
$$\begin{bmatrix} 2 & -1\\ -1 & 2 \end{bmatrix} \begin{bmatrix} x \\ y\end{bmatrix} = \begin{bmatrix} 0 \\3\end{bmatrix}$$
\(AX=b\)
\(A\):系数矩阵,\(X\):未知数向量
解这个方程组可以分别从两个角度考虑:
一是从行的角度。每一行代表了二维平面上的一条直线,那么这个方程组的两行,所代表的两条直线的交点\( (1,2) \),就是这个方程组的解。
另一个是从列的角度考虑。
可以把原方程组写成下面的形式
$$x\begin{bmatrix} 2 \\ -1\end{bmatrix} +y \begin{bmatrix} -1 \\2\end{bmatrix}=\begin{bmatrix} 0 \\3\end{bmatrix}$$
这样就把问题转化成了,要找到正确的线性组合方式
把 \(\begin{bmatrix} 2 \\ -1 \end{bmatrix}\) 和 \(\begin{bmatrix} -1 \\ 2 \end{bmatrix}\) 这两个向量,通过线性组合得到 \(\begin{bmatrix} 0 \\ 3 \end{bmatrix}\)
可以验证\( x=1,y=2\) 是恰好满足的。
找到正确的线性组合(linear combination),是贯穿线性代数课程始终的基本方法。
对于这个例题而言,通过所有 \( x\) 和 \(y \) 的组合,可以得到任 一 \(2\)维的向量。任 一\( 2\)维的向量,从几何方面的反映即是可以布满整个\(2\)维坐标平面。
那么,对于任意的右侧向量 \(b\) ,是否都有解呢?或者换一种表述,对任意\(b\),是否都能求解\(AX=b\) ?
我们从线性组合的角度描述这个问题:\(n\)个列向量的线性组合是否能够覆盖整个\(n\)维空间 ?
考虑\(2\)维的情况,如果是共线的两个向量,那么不管他们两个怎么组合,都得不出线外的向量。
同样\(3\)维的情况下,处于同一平面的\(3\)个向量,不管怎么组合,都得不出平面外的向量。
可以看出,这个问题的本质是,各向量的独立性。
\(n\)维情况下,对于\(AX=b\)是否总能有解,即是否总能通过\(AX\)得到\(b\)?
如果不是相互独立的列向量,这样\(b\)就不是总能求得。有一个向量非独立,那么解就不能覆盖整个\(n\)维空间。如果是\(n\)个相互独立的向量,它们的线性组合则可以覆盖整个\(n\)维空间。
需要关注到的另一个情况:矩阵乘以列向量的方法,按照上面行的角度和列的角度,有两个思考角度。
一种就是矩阵的每一行点乘列向量。这是我们在教材里常见的方法。
另一种就是从列的角度,通过每列的线性组合得出目标矩阵。这是本学习笔记强烈推荐的方法,以后我们遇到矩阵运算的时候,要有意识从列的角度去考虑问题。