What are the uses of a Merkle tree? One use is to provide merkle proof.There are two types of nodes in Bitcoin, full nodes and light nodes. A full node is a node that holds the contents of the entire block, the block header and the block body, which the full node has, and it has the specific information about the transaction. But a light node, like a bitcoin wallet app on your phone, is a light node, and it only keeps the block header, which brings up the question, if you need to prove to a light node that a certain transaction was written to the blockchain, how do you do that? For example, you want to transfer an account to me. You tell me that the transaction in which you transferred money to me has been written to the blockchain and that the payment has been completed. I’m a light node, how do I know if this transaction has been written to the block? It is necessary to use merkle proof to find out where this transaction is. The path from the block where you transferred money to me up to the root node is merkle proof.
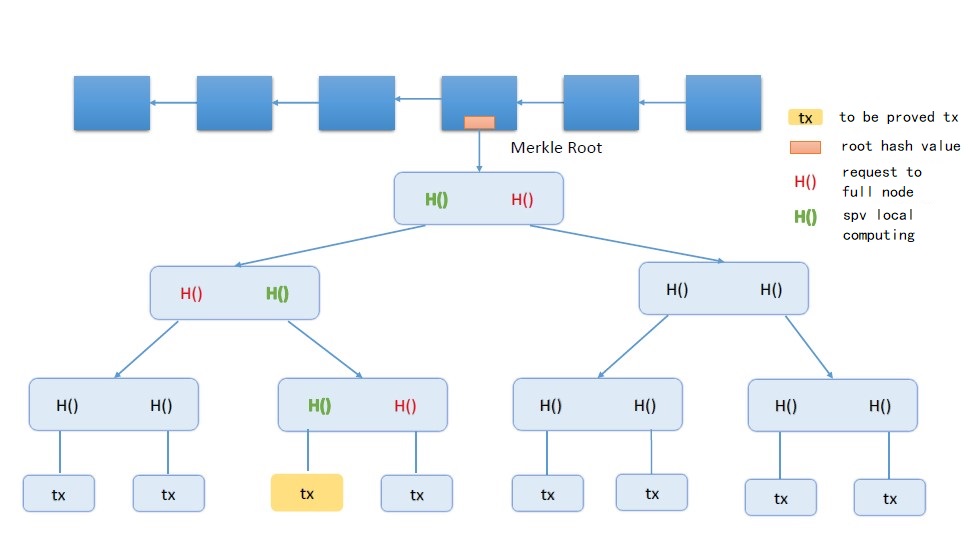
To show this process with the image above, the top row is a small blockchain that shows the merkle tree of one of the blocks, and the bottom row is the transactions it contains. Suppose some light node wants to know if the transaction in yellow is included in this merkle tree. Since the light node does not keep a list of transactions, there is no specific content of the merkle tree, only a root hash value. How can this light node know whether this yellow transaction is included or not? This light node sends a request to a full node for a merkle proof full node that can prove that this yellow transaction is contained in this merkle tree. After receiving this request, just send the three hashes labeled in red in the graph to the light node. With these hashes, the light node can locally compute the three hashes labeled green in the graph. First calculate the hash value of the yellow transaction, that is, the bottom of the green hash, and then and next to the red hash value, that is, the whole node provided by the right side of the red hash value of the splice, you can calculate the upper layer of the node in the green hash, and then and the left side of the layer of the red hash value of the splice can be calculated on the upper layer of the green hash, and so on, you can calculate the the root hash of the whole tree. The light node to the root hash value and block header in the root hash value comparison, you can know the yellow transaction is not in the merkle tree.
After the light node receives such a merkle proof, it only needs to verify from bottom to top that the hash values along the way are correct. If I want to know if the transaction you transferred to me was actually written to this block. As a light node, there’s only the block header, and there’s only the root hash in the block header. Now pass me a path like this, and I check if all these hashes are calculated correctly. Note that when you check, you can only check the hash value on the branch you are on. The hash value of the branch next to it cannot be checked. Since I don’t have the transactions on the next branch, I can’t be sure of the correctness of the hashes on the next branch. As long as I verify that the branch where I have the transactions meets the requirements, and finally take the hash of the root node, and the hash value in the block header that I saved is the same, then it will be fine. It’s the nature of a merkle tree that if a change is made to any part of the tree, it affects the root hash. If the root hash is unchanged, it means that everything in it has not been modified.
To quote. This process seems to be a bit insecure. Because when we verify it we can only verify the branch the transaction is in, there is no way to verify the hash of the branch next to it. This situation seems on the surface to give some freedom to tamper with the data. For example, if someone falsifies the content of a transaction, and the content is changed, the hash value of the block in which it is located is not correct. But the hash of the branch next to it is not verified, and can theoretically take any number. So can I adjust the hash value of the next branch that does not need to be verified, so that the hash finger of the whole node remains unchanged, so that when reflected to the upper layer, the corresponding hash pointer does not need to change.
This is not feasible in practice, the reason is that we talked about in the last section of the article collision resistance nature. This is an artificial hash collision. Even if you give you this degree of freedom, the hash value of the next branch can be arbitrary, but also to create such a hash collision, which is the nature of collision resistance.
The above is the merkle proof can prove that the merkle tree contains a transaction, so this proof is also called proof of member, or called proof of inclusion. for the light node, received such a merkle proof, to verify the complexity of it is how much, the complexity of the time and space is What is the time and space complexity? If there are n transactions in the bottom layer, then the complexity of merkle proof is logarithmic. This is more efficient.
Can we prove that the merkle proof does not contain a transaction, that is, now is the proof of membership, can we prove the proof of non-membership, there is a simplest way to prove, is to pass the whole tree to the light node, the light node receives it, to verify that the construction of the tree are correct, that is, the hash value of each layer is the same as the one of the tree, and the hash value of each layer is the same as the hash value of each layer. The hash values of each layer are correct. It means that there are only these leaf nodes in this tree and no other nodes. The fact that the transaction to be found is not in there proves proof of non-membership. this is a relatively inefficient method, the problem is that its complexity is linear, not logarithmic level. Is there a more efficient way to prove of non-existence. Without making any assumptions about the order in which the leaf nodes are arranged, it is that there is no more efficient method. Because a particular transaction to be found could appear anywhere in the leaf nodes, how do you know that the one you are looking for is not in there unless you send the entire transaction.
But if you do some requirements on the order of these leaf nodes, such as sorting by the hash value of the transaction, taking a hash of the contents of each transaction, and sorting them according to the hash value from smallest to largest, then there is a good method of proving in this way. That transaction to be checked, first calculate a hash, and then see if it is in it, it should be in which position. Let’s say it’s in between some two data blocks, and then what I provide as a merkle proof. It’s that both data blocks go up to the root node. After the light node receives such a proof, verify that the two transactions up the path are correct, and finally the root node calculated hash value has not been modified, it shows that these two nodes in the original merkle tree is indeed neighboring nodes. The transaction to be found should be inserted between these two if it exists, but it does not appear, so it does not exist. This complexity is also logarithmic, at the cost of sorting. This sorted merkle tree is called a sorted merkle tree. bitcoin does not use this sorted merkle tree because bitcoin does not need to do this kind of non-existence proof, there is no such hard requirement, so the merkle tree in bitcoin does not require sorting.
These are the two most basic structures in Bitcoin that we’re going to talk about in this section, a blockchain and a merkle tree, both constructed with hash pointers. What else can hash pointers be used for besides these two structures? Hash pointers can be used instead of regular pointers as long as the data structure is ringless. If there is a ring, there will be certain problems, for example, for a circular chain table, if you use ordinary pointers, it is perfectly legal, but if it is a hash pointer then there will be a problem, it will become a circular dependency, and in the end, which block can not be fixed, there is a loop, so there is a ring can not be, no ring can be used without the case of hash pointers.